|
How the Sand Scorpion Locates Its Prey |

|

|
|
|
|
Philip H. Brownell
J. Leo van Hemmen
Popular Version of Papers
Y3.03
and
Y3.04
As large, day-active and predominantly visual creatures, we humans are slow to appreciate the elegant senses that smaller, nocturnal animals use to find their way around in the dark. The habits of most night-active animals, and their sensory abilities, are largely unknown to us simply because of our inability to observe them directly. A rare exception is the nocturnal sand scorpion from the dunes of the Mojave Desert. These insect-eating arachnids - evolutionary cousins of spiders - fluoresce brilliant yellow-green light under portable blacklights, making them easily the most observable of Nature's night shift. Through studies of these animals we are gaining a new appreciation of the non-visual sensory cues available to animals, and the means by which nervous systems receive, process and interpret the world outside. As burrowing animals, sand scorpions have evolved an exquisite sensitivity to information that comes to them through the surface they live on. The most important of these signals are subtle mechanical vibrations and faint odors in sand that are far below our ability to detect. Specialized vibration sensors on the scorpion's legs guide them to insect prey walking nearby; a unique appendage called the pectine can discriminate, by smell alone, the footsteps left by a prospective mate. An important attribute of the sand dune environment is that it presents and nearly silent sensory backgound for scorpions, a virtual absence of vibrational or chemical 'noise' that might interfere with detection of subtle biological signals. To run this gambit as a nocturnal predator of faster-moving insects, sand scorpions make use of sensory cues we would not expect to find in sand. Sand is a sound-absorbent medium and does not favor conduction of mechanical waves. But over distances of a few decimeters, this natural substrate conducts both surface waves and compressional sound waves through the body of sand. These waves have large enough amplitude and low enough frequency (peak power between 300-400 Hz) to be biologically detectable. Sensors at the tips (tarsi) of the scorpion's eight legs do just that: One sensor, called the basitarsal slit sensillum, detects the surface wave propagated by sand, while others - the numerous sensory hairs touching the surface - are more responsive to compressional waves. As an insect approaches, the vibrational signals it generates tip off the scorpion to its location. In a series of swift and accurate turns, the scorpion moves forward with pincers outstretched until the prey is eventually grasped and stung (Fig. 1).
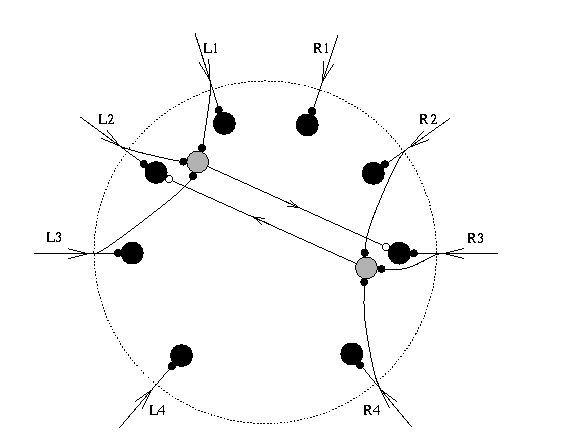
But how does the sand scorpion determine direction of the sand wave source so accurately? We can get a handle on the mechanism of localization by experimentally manipulating the scorpion's sensory experience. One way is to knock out the eight vibration sensors on the legs one at a time, or in patterns that reveal how each sensor contributes to the overall computation of target location. Such manipulations give very systematic changes in the accuracy of the turning response. In the extreme, animals having only one or two intact sensors only respond in one direction, toward the leg with intact sensors. Knowing this we are safe to conclude that target localization is mediated by a definable and mechanistically simple sensory system, one that is open to computational modeling and theoretical analysis. A second experimental test tells us another essential piece of information - that the timing of leg stimulation by the passing surface wave, and not relative amplitude of movement, is the sensory cue that specifies target angle. This is shown experimentally by spanning the legs of the sand scorpion between two independently moveable platforms (Fig. 2) so that time and amplitude of left and right leg movements can be controlled directly. With all of the right legs on one platform and all of the left legs on the other, we can ask the animal "which platform moves first?" - the scorpion answers by turning in that direction. What we learn from this experiment is that a scorpion can tell when some of its sensors are stimulated as little as 0.2 milliseconds before the others. Moreover, even when the "late" platform vibrates at much larger amplitude than the "early" platform (cf. Fig. 2), the scorpion shows its strong preference for the time delay cue over relative intensity of leg stimulation by always turning toward the platform that moves first. A theory to account for the scorpion's prey localizing ability can be developed now as a computational model involving a time window. The model asserts that the surface waves emanating from a target's movements, say a burrowing cockroach 90 degrees to the right of the scorpion, pass beneath the eight points of leg contact with the substrate. This array of vibration sensors is circular (of radius 2-3 cm in adult animals) so that leg R3 (nearest the source) detects the wave first, followed by R4, R2, etc. in turn, until the receptors on the opposite side of the array (on legs L2 and L3) are excited. The neural signals ('spikes') generated by R3's slit sensilla now propagate to a network of second-order neurons in the scorpion's brain. These are arranged in a circular structure analogous to the sensory field. The model assumes that spikes from all sensory neurons propagate to the central processing neurons with identical delay, and that eight command neurons in the brain encode the eight directions of the animal's vibration sensors (see Fig. 3).
The most crucial test of our theoretical model is how well it predicts the turning behavior of animals with various patterns of sensory deficit - the "knock out" experiments described above. Our theory passes this practical test very well, and then goes one step further: Since the slit sensilla and other neurons may, but need not, respond to a passing wave, all that can be, and is, predicted by the model [4] is a probability density for the scorpion's response and its intrinsic scatter. It is natural to ask [5], Can the system's `hardware' be tuned so as to exploit the noise as well as possible? By varying the effectiveness of synaptic excitation and inhibition within the model circuit, a clear but broad minimum appears in the response error. This suggests that evolution through natural selection could fine-tune these central processing networks for optimal performance. For an animal whose ancestors first appeared on earth some 450 million years ago, we might safely assume that it has done so. Supported by National Science Foundation grant (IBN-9320362) and the German Science Foundation (DFG, FG Hörobjekte).
[1] P.H. Brownell, Science 197, 497-482 (1977);
Sci. Am. 251(6) 94-105 (1984)
TU Munich Theoretical Biophysics Homepage
last modified 2007-11-05 by webmaster@Franosch.org |
 Fig. 1. Sand scorpion stinging captured burrowing
cockroach. Photo taken under UV illumination.
Fig. 1. Sand scorpion stinging captured burrowing
cockroach. Photo taken under UV illumination.